
이번 2학년 2학기 기말고사에서 조금 어려워할만한 파트라면 물질의 특성 파트의 ‘재결정’ 파트와 비열과 열팽창 파트의 ‘비열’ 관련 계산이 될 것이다. 실제 난이도는 그리 높지 않은 내용이지만, 그럼에도 불구하고 계산에 익숙하지 않은 학생들이나 과학 자체를 혐오하는 학생들을 다소 스트레스를 받을 파트이기는 하다. 가벼운 마음으로 같이 정리해보고 좋은 결과를 얻어보도록 하자.
1. 기본 개념 모음
① 열량이란 온도가 다른 물체 사이에서 이동하는 열의 양을 의미한다.
쉽게 설명하면
“열의 양”
이 되시겠다.
② 비열의 단위는 칼로리(cal, kcal)이다.
당연하지만 과학에서 사용하는 모든 ‘양’들은 고유한 단위를 가진다.
③ 이 때 1 kcal의 정의는 ‘물 1 kg을 1 ℃ 높이는데 필요한 열량으로 정의한다.
④ 자 여기서 생각해봐야 할 게 있다.
“꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?” “꼭 물이어야만 하나요?”
당연히 아니다.
물이 아닌 어떤 물질로 이야기를 바꿀 때, 우리는 이를 비열이라 하는것이다.
⑤ 비열은 물질마다 다르다. 따라서 물질의 특성이다.
⑥ 비열은 온도 변화와 반비례 관계이다
또한 비열은 그 크기가 클수록 온도를 변하게 하기 위한 열량이 더 많이 필요하다. 즉, 비열은 온도 변화와 반비례 관계이다. 이를 통해 식을 하나 유도할 수 있다.
Q=cmt (열량 = 비열 X 질량 X 온도변화)
공식 암기는 의무이다. 일단 모르겠으면 외우고 다시 글을 열번 백번 정독하기 바란다.
2. 비열 문제 접근 방법론
① 비례 반비례
수업시간에 무지막지하게 강조해온 이야기를 다시 해보겠다. 비례 반비례에 관한 이야기이다. 당연한거 아냐? 라고 생각되면 정상이다. 이게 뭐지? 라고 생각되면 비정상이다. 반박은 받지 않는다.
예컨데 이런 식이 있다고 하면은
A = B X C
1) C 값이 일정할 때, A가 커지면 B도 커진다.
2) B 값이 일정할 때, A가 커지면 C도 커진다.
3) A 값이 일정할 때, B가 커지면 C는 작아진다.
모르겠으면 A B C에 적당한 자연수를 넣어보도록 하자. 그래도 모르겠으면 나도 모르겠다.
아무튼 상술한 식에서의 결론은 다음과 같다.
* 등호가 존재할 때, 등호를 기준으로 좌변과 우변의 변수는 비례관계이다.
* 등호가 존재할 때, 등호를 기준으로 한 변의 서로 다른 두 변수는 반비례관계이다.
말이 어려울수도 있는데, 그렇다면 유감이다.
② 그래프에서 x축과 y축 사이의 관계
한편 과학에서는 그래프의 해석에 대한 문제가 자주 출제되며, 그렇기에 수업시간에 귀에 못이 박히도록 때려박은 이야기가 있다. 바로 그래프에서 x축과 y축 사이의 관계이다.
나는 수학강사가 아니지만, 일차함수는 수학이라고 말하기에는 과학의 너무 많은 분야에서 사용된다. 그렇기에 일차함수에 한해서는 과학 수업시간에도 보충 설명을 하고는 한다.
‘함수’란 뭘까. 수학적인 정의를 깊게 들어가자는 말은 아니다. 전하고자 하는 핵심은, x값이 변함에 따라 정해지는 y값이다. 다시 말하면 x값은 변화를 일으키는 원인이 되고, y값은 그 변화에 대응하는 결과가 된다. 이를 선형적으로 표현하면 일차함수라 부르는 것이다.
아무튼, 잔소리는 여기까지 하고 본격적으로 문제에 관해 논해보겠다.
③ 같은 열량을 가하는 경우

예컨데 이런 문제이다. 이런 문제를 보면 당신이 해야 하는 생각은 딱 두개이다.
" Q=cmt 에서 Q가 같은 상황이구나 "
" A~C는 온도가 오르는 정도가 다르구나. 그럼 c나 m에 차이가 있겠네 "
그리고 문제를 보는거다.
(1) A, B, C가 같은 물질이란다. 그럼 우리가 해야하는 생각은 뭐겠나.
“ 아 비열이 같네 ”
이지하다.
결국 그렇다면 m과 t는 반비례함을 알 수 있다. 즉 질량이 가장 크다는 것은, 온도 변화가 가장 작다는 것이고, 그래프의 기울기가 가장 낮다는 것이다.
(2) A, B, C의 질량이 같단다. 그럼 우리가 해야하는 생각은 뭐겠나.
“ 아 비열에 차이가 있었겠네 ”
매우 이지하다.
결국 그렇다면 c와 t는 반비례함을 알 수 있다. 즉 비열이 가장 크다는 것은, 온도 변화가 가장 작다는 것이고, 그래프의 기울기가 가장 낮다는 것이다.
이 설명이 이해가 되지 않았다면 위의 ①과 ②를 다시 읽는다. 그리고 ③을 다시 확인한 후 이해가 되지 않으면 위를 반복해라..

생각해라
“같은 물질이래”
“그럼 비열이 같겠네”
“근데 온도변화가 다르네”
“그럼 질량이 다르겠네”
“A는 60도 올랐네”
“B는 20도 올랐고”
“그럼 온도변화가 3 : 1이니깐, 질량비는 1 : 3이겠다. 반비례하니깐”
일부로 구어체로 적었다. 따라해보기 좋게. 반복해서 읽어보는 것도 추천한다. 공부 방법론은 사실 개인의 취향에 가깝기 때문에 내가 뭐라 왈가왈부 할만한 이야기는 아닌 것 같기는 하다.
④ 온도가 다른 두 물체를 접촉하는 경우
이전 단원에서 우리는 열평형에 대해서 러프하게 배웠다. 열평형에서 비열의 관점을 넣는 것 뿐이다. 어려울 건 없다.
다시 생각을 때려보자. 먼저 문제를 읽는거다.
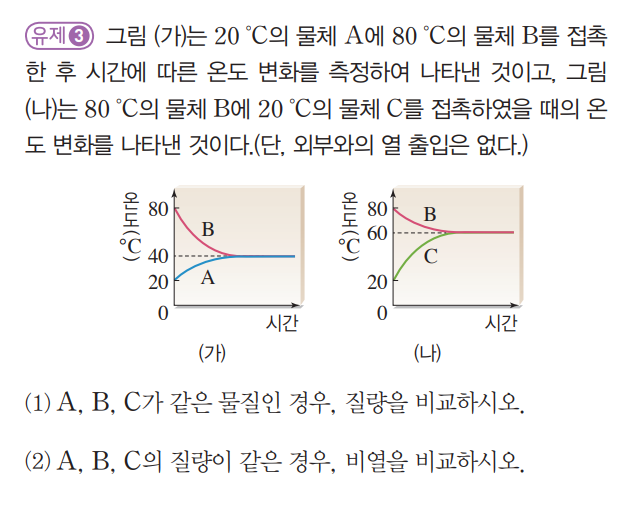
(1) A B C가 같은 물질인 경우
“비열이 같겠다”
“(가) 그래프를 보니 A는 20도 오르고 B는 40도 떨어졌네”
“그럼 질량이 다르겠다”
“온도변화가 1 : 2니깐 질량비는 2 : 1이겠네”
“(나) 그래프를 보니 B는 20도 떨어지고 C는 40도 올라가네”
“온도변화가 1 : 2니깐 질량비는 2 : 1이겠네”
“그럼 A B C의 질량비는 4 : 2 : 1 이겠다”
쉽다. 매우 쉽다.
(1) A B C가 질량이 같은 경우
“(가) 그래프를 보니 A는 20도 오르고 B는 40도 떨어졌네”
“그럼 비열이 다르겠다”
“온도변화가 1 : 2니깐 비열비는 2 : 1이겠네”
“(나) 그래프를 보니 B는 20도 떨어지고 C는 40도 올라가네”
“온도변화가 1 : 2니깐 비열비는 2 : 1이겠네”
“그럼 A B C의 비열비는 4 : 2 : 1 이겠다”
사고방식의 전개과정이 아예 똑같다는게 느껴지는가? 그렇다면 다행이고..
Edited 2024.11.15
Edited by 푸른삿포로
'# 중등과학 > 중2 - 내신적 해석법' 카테고리의 다른 글
| [2024] V-I-1. 소화 내신적 해석 (1) | 2024.09.19 |
|---|---|
| [2023] 2-I-3. 이온 문제풀이 (0) | 2022.12.26 |
| [2023] 2-I-2. 원자와 분자 오투 문제풀이 (0) | 2022.12.18 |
| [2023] 2-I-1. 물질의 구성 오투 문제풀이 (1) | 2022.12.17 |
| 01. 원소 파트 출제논점 (0) | 2021.05.04 |




댓글